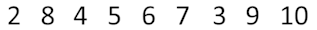В честь юбилея ректорат ЮФУ решил запустить акцию «Сто и десять кексов». В каждом корпусе университета открылась лавка с кексами, в которой каждый студент может получить бесплатные кексы.
Не прошло и пары минут после открытия, как к лавкам набежали студенты и образовалось много очередей. Но самая большая очередь образовалась в главном корпусе ЮФУ. Изначально в этой очереди стояло $$$n$$$ студентов, но потом в течение следующих $$$m$$$ минут какие-то студенты приходили и вставали в очередь, а какие-то уходили.
За каждым студентом закреплен номер его зачетной книжки, будем называть это число номером студента. У каждого студента будет уникальный номер, по которому можно однозначно его идентифицировать. Будем считать, что каждую минуту происходило одно из следующих событий:
- Студент с номером $$$x$$$ пришел и встал перед студентом с номером $$$y$$$;
- Студент с номером $$$x$$$ пришел и встал в конец очереди;
- Студент с номером $$$x$$$ ушел из очереди; возможно, он потом вернется.
Аналитикам стало интересно, а какой будет очередь после $$$m$$$ минут?
Помогите им и сообщите конечное состояние очереди.
В первой строке заданы два целых числа $$$n$$$ и $$$m$$$ $$$(1 \le n, m \le 10^5)$$$ — текущее число студентов в очереди и количество изменений.
В следующей строке задается $$$n$$$ целых различных чисел $$$a_1, a_2, \cdots , a_n$$$ $$$(1 \le a_i \le 10^9)$$$, где $$$a_i$$$ — номер студента, который стоит на $$$i$$$-й позиции в очереди.
В следующих $$$m$$$ строках идет описание запросов изменения очереди.
В каждой строке в зависимости от типа запроса задается два или три числа. Первое число $$$t_j$$$ $$$(1 \le t_j \le 3)$$$ — тип события, которое произошло в $$$j$$$-ю минуту.
Если $$$t_j = \textbf{1}$$$, то в строке задается еще 2 числа $$$x$$$ $$$(1 \le x_j \le 10^9)$$$ и $$$y$$$ $$$(1 \le y_j \le 10^9)$$$ — номер студента, который пришел, и номер студента, перед которым он встанет в очереди. Гарантируется, что студент с номером $$$x$$$ ещё не занял очередь, а студент с номером $$$y$$$ уже стоит в ней.
Если $$$t_j = \textbf{2}$$$, то в строке задается еще 1 число $$$x$$$ $$$(1 \le x_j \le 10^9)$$$ — номер студента, который пришел и встал в конец очереди. Гарантируется, что студент с номером $$$x$$$ ещё не занял очередь.
Если $$$t_j = \textbf{3}$$$, то в строке задается еще 1 число $$$x$$$ $$$(1 \le x_j \le 10^9)$$$ — номер студента, который ушел из очереди. Гарантируется, что студент с номером $$$x$$$ стоит в очереди.
В первой строке выведите одно число $$$|a|$$$ — длину очереди после выполнения всех запросов изменения.
В следующей строке выведите $$$|a|$$$ чисел $$$a_1, a_2, \cdots , a_{|a|}$$$, где $$$a_i$$$ — номер студента, который стоит на $$$i$$$-й позиции в очереди.
7 61 2 3 4 5 6 71 8 32 93 31 3 92 103 1
9 2 8 4 5 6 7 3 9 10
Изначально очередь выглядит следующим образом:
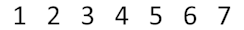
В первую минуту приходит студент с номером 8 и встает перед студентом с номером 3.
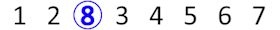
Потом студент с номером 9 встает в конец очереди.
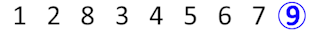
Студент с номером 3 уходит из очереди.
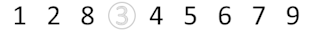
Потом он возвращается и становится перед студентом с номером 9.
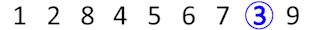
После в конец очереди становится студент с номером 10.
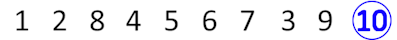
И студент с номером 1 уходит из очереди.
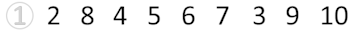
После $$$m$$$ событий очередь имеет следующий вид: